Superficies y volúmenes

Superficie

Configuración geométrica que posee solo dos dimensiones.

superficie

Clasificación de las Superficies

Entre las superficies principales se pueden mencionar:

Superficie reglada

Superficie generada por el movimiento de una recta, denominada generatriz, manteniéndose en contacto con otra u otras líneas, denominadas directrices, cumpliendo además en su desplazamiento ciertas condiciones particulares.

superficie reglada

Superficie de curvatura simple

Superficie reglada en la cual cada dos posiciones adyacentes de la generatriz (g) son coplanares (son paralelas o se cortan).

Las superficies de curvatura simple son superficies desarrollables, es decir, pueden extenderse sobre un plano. Ejemplos de estas superficies son:

• superficie cilindrica: superficie generada por el movimiento de una generatriz (g) que se mantiene en contacto con una directriz (d) curva, siendo además paralelas todas las posiciones de la generatriz; se clasifican en:
  • superficie cilindrica de revolución: superficie cilíndrica en la cual todas las posiciones de la generatriz (g) equidistan de un eje (e), paralelo a ella,
  • superficie cilindrica de nó revolución: superficie cilíndrica en la cual no es posible definir un eje (e) que equidiste de todas las posiciones de la generatriz (g),
• superficie cónica: superficie reglada generada por el movimiento de una generatriz (g), manteniéndose en contacto con una directriz (d) curva, teniendo, todas las posiciones de la generatriz (g), un punto común (V), denominado vértice; se clasifican en:
  • superficie cónica de revolución: superficie cónica en la cual, todas las posiciones de la generatriz (g), forman el mismo ángulo con un eje (e), que pasa por el vértice (V),
  • superficie cónica de nó revolución: superficie cónica en la cual no es posible definir un eje (e), que forme el mismo ángulo con todas las posiciones de la generatriz.

superficie de curvatura simple

Superficie alabeada

Es una superficie reglada nó desarrollable, es decir, en la cual, dos posiciones sucesivas de la generatriz no son coplanares. Entre este tipo de superficies, se puede citar:

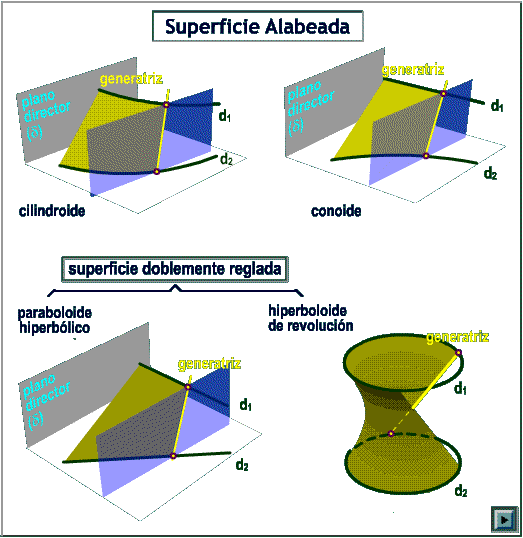
• cilindroide: la generatriz (g) se desplaza manteniéndose paralela a un plano director (d) y apoyada sobre dos directrices (d₁ y d₂) curvas,
• conoide: la generatriz (g) se desplaza manteniéndose paralela a un plano director (d) y apoyada sobre dos directrices, siendo una de ellas recta (d₁) y la otra curva (d₂).
• Superficie doblemente reglada: Superficie alabeada en la cual por cada uno de sus puntos pasan dos generatrices (g₁ y g₂). Entre ellas se pueden citar:
  • paraboloide hiperbólico: la generatriz (g) se desplaza manteniéndose paralela a un plano director (d) y apoyada sobre dos directrices rectas (d₁ y d₂) que se cruzan,
  • hiperboloide de revolución: la generatriz (g) se apoya sobre dos directrices (d₁ y d₂) circulares, paralelas, y se mueve manteniendo constante el ángulo (a⁰) que forma ellas.

Superficie de curvatura doble

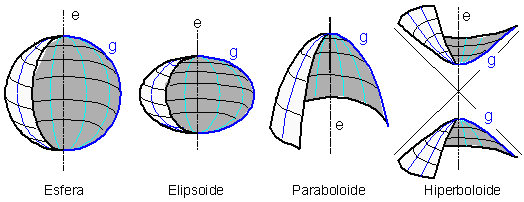
Son superficies generadas por el movimiento de una generatriz (g) curva. Estas superficies no contienen líneas rectas y por lo tanto no son desarrollables. Entre ellas son muy conocidas las cuádricas, las cuales son superficies generadas por la rotación de una curva cónica alrededor de uno de sus ejes. Las cuádricas son:

• esfera: la generatriz (g) es una circunferencia,
• elipsoide: la generatriz (g) es una elipse,
• paraboloide: la generatriz (g) es una parábola,
• hiperboloide: La generatriz (g) es una hipérbola.

superficie de curvatura doble 

Construcción de polígonos mediante el compás.

  Mediante la aplicación de los conceptos referentes a los ángulos de los polígonos, es posible servirse del instrumento de dibujo que es el compás, para construir graficamente diversos polígonos.

El compás es un instrumento básicamente aplicable en el trazado de circunferencias, que delimitan una figura plana que es el círculo; el cual puede ser considerado un tipo especial de polígono regular, en el cual todos sus lados están constituídos solamente por un punto, y cuya dimensión está determinada por la longitud del radio, que es equivalente a la abertura del compás.

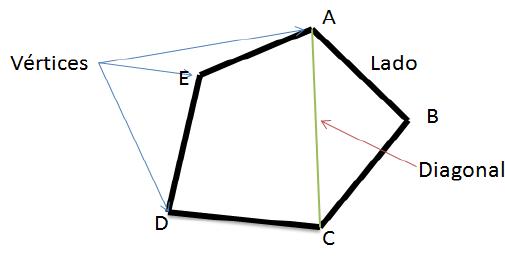
El método a utilizar para construir polígonos mediante el uso del compás, se basa en determinar los vértices de los lados del polígono, estableciendo en qué puntos de la circunsferencia deben situarse para que el polígono resulte inscripto en ella.

Esa determinación se realiza a partir del conocimiento de los valores de los ángulos centrales del polígono que se desea construir.

 Para trazar un triángulo equilátero inscripto en un círculo, manteniendo el radio (abertura del compás) empleado para trazar el círculo, se determina un punto de la circunferencia (preferiblemente en la vertical inferior de su centro), y centrando en ese punto se traza un arco con extremos en la circunsferencia.

Los puntos de intersección (A y B) determinan un lado del triángulo equilátero; por lo cual tomando la medida de ese segmento con el compás y trasladándola sobre la parte superior de la circunferencia, se determinará el vértice (C) de unión de los otros dos lados.

 

 Para trazar un cuadrado inscripto en un círculo, se traza una recta que pasando por el centro llegue a la circunsferencia en sus extremos (diámetro AB).

Con una abertura del compás mayor a la empleada para trazar el círculo, centrando en los puntos extremos del diámetro, se marcan puntos en la circunferencia; lo que determinará dos nuevos puntos (C y D). Uniéndolos mediante una recta, resultará un nuevo diámetro perpendicular al anterior; cuyos puntos de contacto con la circunferencia serán los vértices del cuadrado inscripto.

Como el cuadrado inscripto queda en posición transversal, puede trazarse otro con los lados en posición horizontal y vertical, simplemente trazando las medianas del cuadrado anterior, para determinar los vértices A', B', C' y D', de un nuevo cuadrado inscripto en el mismo círculo.

 Para trazar un exágono inscripto en un círculo, se fija un punto sobre la circunferencia, y con la misma abertura del compás, se marcan puntos haciendo centro primero en ese punto y luego sucesivamente en los nuevos puntos.

Ello determinará que se marquen sobre la circunferencia los seis puntos que corresponden a los vértices del exágono.

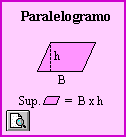
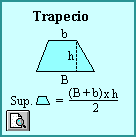
CALCULO de SUPERFICIES

Los polígonos son equivalentes cuando tienen la misma superficie, aunque tengan  distinta forma. Esta propiedad es de suma utilidad para calcular la superficie de  diferentes polígonos.

Volumen

El volumen es el espacio que ocupan los cuerpos.

Los cuerpos geométricos existen en el espacio y son por lo tanto objetos que tienen tres dimensiones (ancho, alto y largo) limitados por una o más superficies. Si todas las superficies son planas y de contorno poligonal, el cuerpo es un poliedro. Si el cuerpo no está limitado por polígonos, sino por superficies curvadas recibe el nombre de cuerpos redondos.

La fórmula para  calcular el volumen de un cuerpo depende de su forma.

Para medir el volumen de un cuerpo se utilizan unidades cúbicas, que son: milímetro cúbico, centímetro cúbico, decímetro cúbico y metro cúbico

Definición

Un Sólido o Cuerpo Geométrico es una figura geométrica de tres dimensiones (largo, ancho y alto), que ocupa un lugar en el espacio y en consecuencia tiene un volumen.

Los cuerpos geométricos tridimensionales ocupan siempre un espacio. La medida de ese espacio recibe el nombre de volumen. Asimismo, los cuerpos que están huecos pueden albergar en su interior otros cuerpos (sólidos, líquidos o gaseosos) en una cantidad que recibe el nombre de capacidad.

Cuando estudiamos las áreas hablábamos de dos dimensiones: largo y ancho. El producto de los valores largo X ancho nos da el área.
Para calcular un volumen necesitamos tres dimensiones: largo, ancho y alto. El producto de los valores largo X ancho X alto nos da el volumen.
Es lo mismo que decir, el volumen lo calculamos también multiplicando el área de la base por la altura.

http://webdelprofesor.ula.ve/nucleotrujillo/alperez/teoria/cap_01a-conceptos_geometricos/05-superficie.htm#supregala

http://www.escolar.com/geometr/11calcu.htm

http://www.escueladigital.com.uy/geometria/4_figplanas.htm#construccion

http://poligonomodular.blogspot.mx/2011/01/definicion-de-solidos-geometricos.html

http://www.aula365.com/post/los-cuerpos-geometricos/

Polígonos

Polígono Regular
	Si todos los ángulos son iguales y todos los lados son iguales, entonces es un polígono regular (de otra forma es "irregular"). Este es un pentágono regular

Elementos de un polígono

Lados: son cada uno de los segmentos que limitan el polígono.

Vértices: son los puntos en los que se unen los lados.

Ángulos: porción de plano comprendida entre dos lados y un vértice común.

Diagonal: segmento de recta que une dos vértices no consecutivos.

Un polígono es una figura geométrica plana limitada por un número finito de líneas rectas conectadas que forman una figura cerrada. Los puntos donde dos líneas rectas del polígono se unen son los vértices.

Tipos de polígonos

Los polígonos se pueden clasificar mediante cuatro criterios diferentes

Según sus lados

• Triángulo: polígono con tres lados
• Cuadrilátero: polígono con cuatro lados
• Pentágono: polígono con cinco lados
• Hexágono: polígono con seis lados
• Heptágono: polígono con siete lados
• Octógono: polígono con ocho lados
• Eneágono: polígono con nueve lados
• Decágono: polígono con diez lados
• Undecágono: polígono con once lados
• Dodecágono: polígono con doce lados

Según su regularidad

• Equilátero: si tienen todos sus lados iguales
• Equiángulo: si tiene todos sus lados iguales
• Regular: si todos los lados son iguales y es equiángulo (todos los ángulos iguales)

Según sus ángulos

• Convexo: todos sus ángulos interiores tienen menos de 180º (o también si existe alguna recta que lo corte en más de dos puntos)
• Concavo: algún ángulo interior tiene más de 180º

Según su complejidad

• Simple: ningún costado del polígono intersecta con otro
• Complejo: al menos un par de costados se corta

Diagonales de un polígono

Las diagonales de un polígono son segmentos que unen dos vértices no consecutivos.

El número de diagonales (D) viene determinado por el número de lados que tiene el polígono. Su fórmula es:

Suma de los ángulos interiores

En todos los polígonos convexos, la suma (Θ) de los ángulos interiores (α) viene determinada por el número de lados (N) que tiene éste.

La fórmula que determina dicha suma (en grados sexagesimales) es:

Por lo tanto, cada ángulo interior (α) de un polígono regular será:

Apotema de un polígono regular

La apotema de un polígono regular puede obtenerse sabiendo el número de lados (N) del polígono y lo que mide cada lado (L).

Sea el ángulo central α el ángulo que forman las dos líneas que unen el centro del polígono (O) y dos vértices consecutivos. Éste se calcula como:

Mediante la tangente de la mitad del ángulo central y un lado (L), se calcula la apotema (ap) del polígono regular.

http://www.disfrutalasmatematicas.com/definiciones/poligono-regular.html

http://www.ceibal.edu.uy/contenidos/areas_conocimiento/mat/cuadrilateros/elementos_de_un_polgono.html

http://www.universoformulas.com/matematicas/geometria/poligono/

http://www.imagui.com/a/formulas-area-y-perimetro-iKdAoagez

Glosario

Punto es el objeto fundamental en geometría, el punto representa solo posición y no tiene dimensión, es decir, largo cero, ancho cero y altura cero. Se representan por letras mayúsculas.

Ejemplo:

Tres puntos

Recta tiene solo longitud, no tiene ancho ni altura ni grosor. Es un conjunto infinito de puntos que se extienden en una dimensión en ambas direcciones. Una recta se puede representar por:

Semirrecta la definimos como la porción de una recta que tiene principio pero no tiene fin.

segmento de recta es una porción de la recta con principio y con fin, es decir sabemos donde empieza y donde termina por ende lo podemos medir.

Plano tiene ancho y largo, sin altura ni grosor. Un plano es una superficie en dos dimensiones, se puede pensar como un conjunto de puntos infinitos en dos dimensiones.

Vértices: puntos finales de los segmentos que forma el polígono, en la figura: A, B, C, D, E.
Lados: segmentos de recta que unen dos vértices consecutivos del polígono, en la figura los lados son: AB,
Lados consecutivos: cualquier par de lados que comparten un vértice, en la figura: AB y BC, BC y CD,
Diagonal: un segmento de recta que une dos vértices no consecutivos, en la figura: AC.
Apotema: de un polígono regular es la menor distancia entre el centro y cualquiera de sus lados. Es un segmento cuyos extremos son el centro de un polígono regular y el punto medio de uno cualquiera de sus lados, y es siempre perpendicular a dicho lado.

Geometría

La geometría es una parte de la matematica que trata de estudiar unas idealizaciones del espacio en que vivimos, que son los puntos, las rectas y los planos, y otros elementos conceptuales derivados de ellos, como poligonos o poliedros.

En la practica, la geometría sirve para solucionar problemas concretos en el mundo de lo visible. Entre sus utilidades se encuentran la justificación teorica de muchos instrumentos: compás, teodolito, pantógrafo, sistema de posicionamiento global. También es la que nos permite medir areas y volumenes, es útil en la preparación de diseños, e incluso en la fabricación de artesanías.

 Euclides

Euclides es, sin lugar a dudas, el Matemático más famoso de la antigüedad y quizás el más nombrado y conocido de la historia de las Matemáticas.

Se conoce poco de la vida de Euclides, sin embargo, su obra sí es ampliamente conocida. Todo lo que sabemos de su vida nos ha llegado a través de los comentarios de un historiador griego llamado Proclo. Sabemos que vivió en Alejandría (Egipto), al parecer en torno al año 300 a.c. Allí fundó una escuela de estudios matemáticos. Por otra parte también se dice que estudió en la escuela fundada por Platón.

Su obra más importante es un tratado de geometría que recibe el título de "Los Elementos", cuyo contenido se ha estado (y aún se sigue de alguna manera) enseñando hasta el siglo XVIII, cuando aparecen las geometrías no euclídeas. 

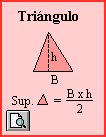
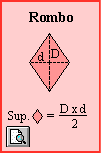
 La geometria clásica o axiomática es una matemática en la cuál los objetos, en vez de ser números, son puntos, rectas, planos y otras figuras definidas en función de estas.

Teniendo en cuenta más axiomas se obtienen otras geometrías (en las cuales todo lo dicho hasta aquí es válido). Si damos por cierto el axioma del paralelismo de Euclides, obtenemos la Geometría euclidiana también conocida como geometría plana.

Agregando a estos los axiomas relativos al espacio, obtenemos la geometría espacial (estos últimos no son más que extensiones de los axiomas relativos al plano). La Geometría descriptiva, es la que se encarga de que los problemas posibilitar la resolución de los problemas de la geometría del espacio por medio de operaciones efectuadas en un plano.

Si agregamos otros axiomas, ya sean diferentes postulados de paralelismo o de existencia de conjuntos de puntos mayores que el plano (y menores que el espacio) se obtienen las geometrías no euclídeas

Útilizando los conocimientos de otras areas (y por lo tanto sus axiomas respectivos), se obtienen: la Geometría analítica, los métodos del álgebra y del análisis matemático.

La Geometría Analítica, es fundamental para el estudio y desarrollo de nuevos materiales que nos facilitan la vida diaria, razón por la cual esta asignatura siempre influye en la vida de todo ser humano.

El objetivo del presente trabajo es ayudar al estudiante del tercer curso curso de Geometría Analítica a comprender de qué manera se relaciona esta asignatura con su entorno, con las actividades que realiza y consigo mismo.

La Ecuación de la Recta, La Ecuación de la Circunferencia, La Ecuación del Elipse, La Ecuación de la Parábola y La Ecuación de la Hipérbola en sus diferentes representaciones (en el origen, fuera del origen y su forma general), son las cinco grandes temáticas en torno a las cuales se centrarán las actividades de aprendizaje en este curso.

Partiendo de que La Geometría Analítica, estudia las figuras geométricas utilizando un sistema de coordenadas y resuelve los problemas geométricos por métodos algebraicos, donde las coordenadas se representan por grupos numéricos y las figuras por ecuaciones, abordaremos las temáticas anteriores partiendo de esta definición.

Geometría y Diseñadores Gráficos.

Algunos usan la combinación de Formas y Líneas para formar composiciones detalladas, a menudo mezcladas con elementos de otros géneros artísticos para formar una gran variedad de Diseños Individuales y Únicos en estilos.

La Pura Forma Geométrica ha sido una Herramienta Básica para los Artistas a lo largo de la historia y todavía se utiliza como algo destacado por los Diseñadores y Artistas de hoy en dia.

http://www.cecyt3.ipn.mx/actividades-on-line/ganalitica/geometria_analitica%20apuntes.pdfhttp://www.culturageneral.net/matematicas/definicion_geometria.htm

http://www.um.es/docencia/pherrero/mathis/euclides/euclid.htm
http://www.juanmiguelsalas.com/blog/2011/01/geometria-en-ejemplos-de-diseno-grafico/